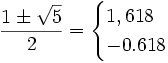u₁, u₂ …, u_n (1)

in cui ogni termine è la somma dei due termini precedenti; cioè per ogni n maggiore di 2,

u_n = u_n-1 + u_n-2 (2)

Successioni di questo tipo, in cui ogni termine è definito come una certa funzione dei termini precedenti, s’incontrano di frequente in matematica e sono chiamate successioni ricorrenti.

In aggiunta alla condizione (2), per determinare i termini di una successione ricorrente è indispensabile conoscerne i primi due; procedendo in tal modo è possibile raggiungere termini di indice arbitrariamente grandi e determinarli. La sequenza di Fibonacci descritta in precedenza è proprio un esempio di successione ricorrente in cui u₁ = u₂ = 1 ed i suoi termini, aventi una notevole gamma di proprietà e applicazioni, sono detti numeri di Fibonacci.

Se si sommano due o più numeri consecutivi di tale serie, sempre a partire da A, e si aggiunge ulteriormente "1", si ottiene sempre un altro numero di Fibonacci che nella sequenza segue di due posti l'ultimo termine della somma

( A+B+C+1 = E )

Esempi:

1+1+2+3+5+1 = 13

In questo caso si sono sommati i primi cinque numeri di Fibonacci, si è aggiunto uno e si è ottenuto il settimo numero della sequenza.

1+1+2+3+5+8+13+21+34+55+89+1=233
In questo caso invece si sono sommati i primi undici numeri di Fibonacci, si è aggiunto uno e si è ottenuto il tredicesimo numero della sequenza.

Inoltre se si prendono due numeri di Fibonacci consecutivi e se ne fa il quadrato, la somma fra i quadrati è un altro numero di Fibonacci che nella sequenza occupa il posto risultante dalla somma delle posizioni dei due termini di partenza.

Esempi:

3²+5²=34
In questo caso si sono presi il quarto e il quinto numero della sequenza, se ne è fatto il quadrato e la somma fra i quadrati è risultata essere il nono numero di Fibonacci.

8²+13²= 233

In questo caso si sono presi il sesto e il settimo numero della sequenza e la somma fra i loro quadrati ha dato il tredicesimo numero di Fibonacci.
 

a = bq + r e 0<r<b

Prendiamo come esempio i seguenti numeri di Fibonacci:

6765 = 610 x 11 + 65

610 = 55 x 11 + 5

55 = 5 x 11

Il fatto che il massimo comun divisore di questi due numeri di Fibonacci sia ancora un numero di Fibonacci, il 5, non è pura coincidenza.
 

DEFINIZIONE GEOMETRICA
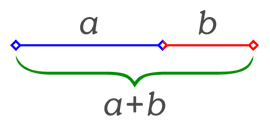
Ripartizione di un segmento in due parti, che stanno tra loro come la maggiore (a) sta al segmento intero (1); utilizzando i simboli si ha: 1:a=a:b.

Se AB è il segmento dato, si conduca la per perpendicolare ad AB nell’estremo B e si prenda su di esso il segmento BO, metà di AB, indi col centro in O si descriva la circonferenza di raggio OB, che risulterà tangente in B alla retta AB. Si unisca A con O e si chiamino C e D le intersezioni della retta AO con la circonferenza; si porti infine su AB il segmento AE congruente ad AC. Proveremo che AE è il segmento cercato, cioè che sussiste la proporzione:

AB : AE = AE : EB

Infatti per il teorema della secante e della tangente (se da un punto si conducono ad una circonferenza una secante e una tangente, il segmento determinato dalla circonferenza sulla tangente è medio proporzionale fra i segmenti determinati sulla secante e aventi un estremo in quel punto) si ha:

AD : AB = AB : AC

Da cui scomponendo si ottiene:
(AD – AB) : AB = (AB – AC) : AC
Ma siccome AB è congruente a CD e AC è congruente ad AE si ha pure:
AD – AB = AD – CD = AC = AE
AB – AC = AB – AE =EB
Perciò l’ultima proporzione diventa:
AE : AB = EB : AE
Da cui invertendo:
AB : AE = AE : EB 

RETTANGOLO AUREO

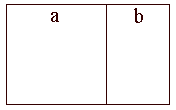
Esiste uno speciale rettangolo le cui proporzioni corrispondono alla sezione aurea. Il suo nome è rettangolo aureo. Per costruire il rettangolo aureo si disegni un quadrato di lato a i cui vertici chiameremo, a partire dal vertice in alto a sinistra e procedendo in senso orario, AEFD. Quindi dividere il segmento AE in due chiamando il punto medio A'. Utilizzando il compasso e puntando in A' disegnare un arco che da F intersechi il prolungamento del segmento AE in B. Con una squadra disegnare il segmento BC perpendicolare ad AB. Il rettangolo ABCD è un rettangolo aureo nel quale Ab è diviso dal punto E esattamente nella sezione aurea:

AE:AB=EB:AE 

TRIANGOLO CON ANGOLI DI MISURA: 72°, 72°, 36°.

Dato un triangolo isoscele i cui angoli alla base misurano 72° ciascuno, e l’angolo al vertice misura 36°, la bisettrice di un angolo alla base divide il lato obliquo opposto nel punto d’intersezione in due segmenti in modo tale da creare una sezione aurea. Infatti il triangolo ABC è simile al triangolo BCD. E da questo risulta che:

AC:BC=BD:DC

e dunque:

AC:AD=AD:DC

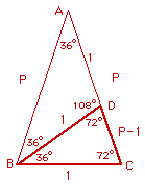
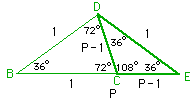
TRIANGOLO CON ANGOLI DI MISURA: 36°, 36°, 108°.

Dato un triangolo isoscele i cui angoli alla base misurano 36° ciascuno, e l’angolo al vertice misura 108°, il lato obliquo e la differenza tra la base e il lato obliquo danno vita a una sezione aurea. Infatti il triangolo CDE è simile al triangolo ABD della figura precedente. 

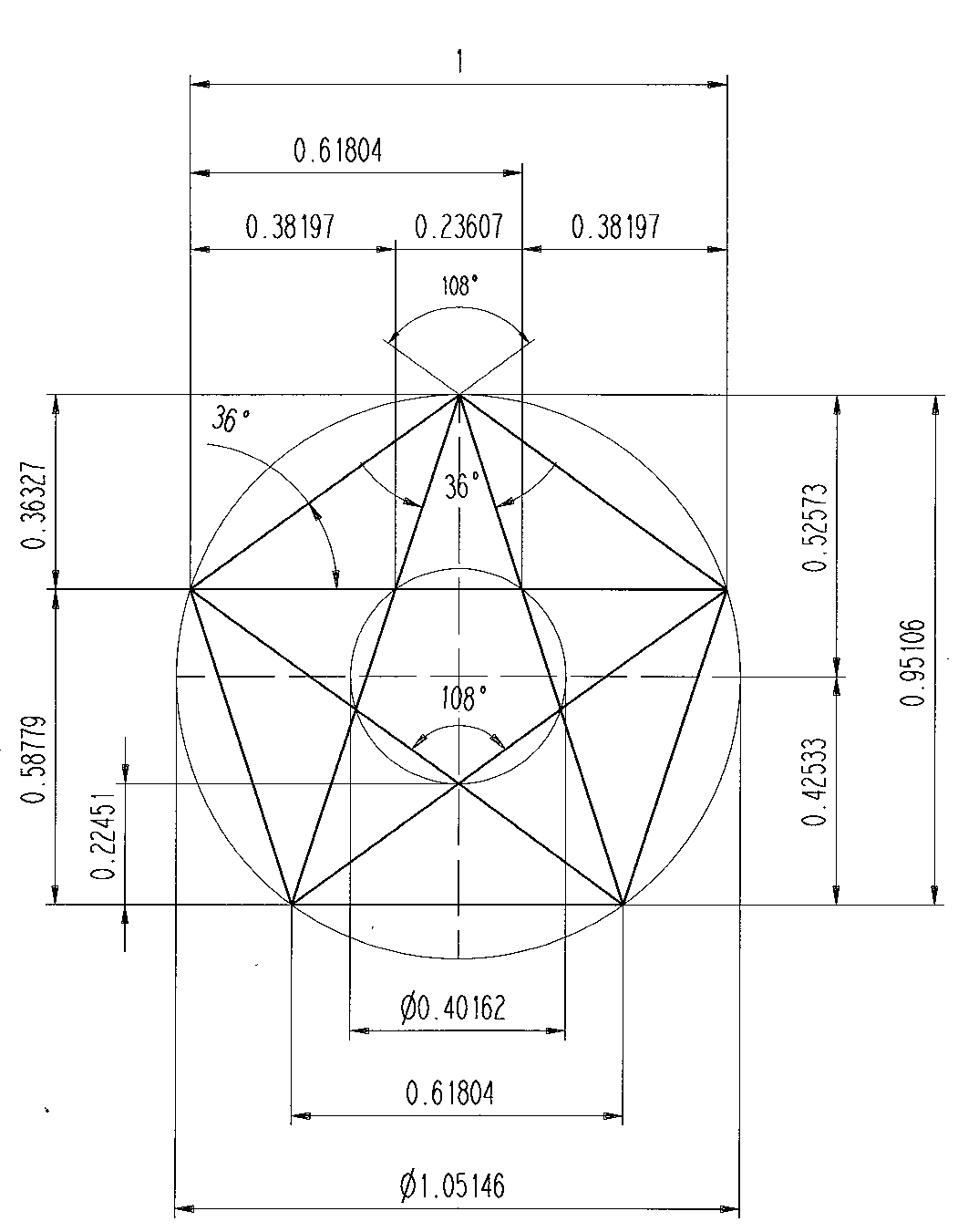
PENTAGONO E TRIANGOLI IN ESSO CONTENUTI

All’interno di un pentagono, ogni lato forma con due diagonali (il segmento che unisce due punti non adiacenti) un triangolo dagli angoli con misura 72°, 72°, 36°, con le proprietà spiegate in precedenza. Ogni lato forma, con il punto d’incontro di due diagonali consecutive, un triangolo dagli angoli 36°, 36°, 108°, con le proprietà descritte in precedenza. Cioè il lato del pentagono regolare è la sezione aurea di una sua diagonale e il punto d' intersezione tra due diagonali divide ciascuna di esse in due segmenti che stanno nel rapporto aureo. 

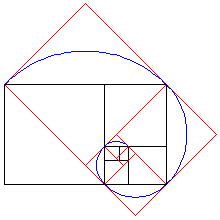
SPIRALE AUREA

Se all’interno di un rettangolo aureo si disegna un quadrato con lato uguale al lato minore del rettangolo, il rettangolo differenza sarà anch’esso un rettangolo aureo. Si ripeta l’operazione per almeno cinque volte al fine di avere un effetto visivo adeguato. Si punti la punta del compasso sul vertice del quadrato che giace sul lato lungo del rettangolo e si tracci l’arco che unisce i gli estremi dei due lati che formano l'angolo scelto. Si ripete l'operazione per ogni quadrato disegnato in modo da creare una linea continua.